111
QUADERNI DI
ORIENTAMENTO
40
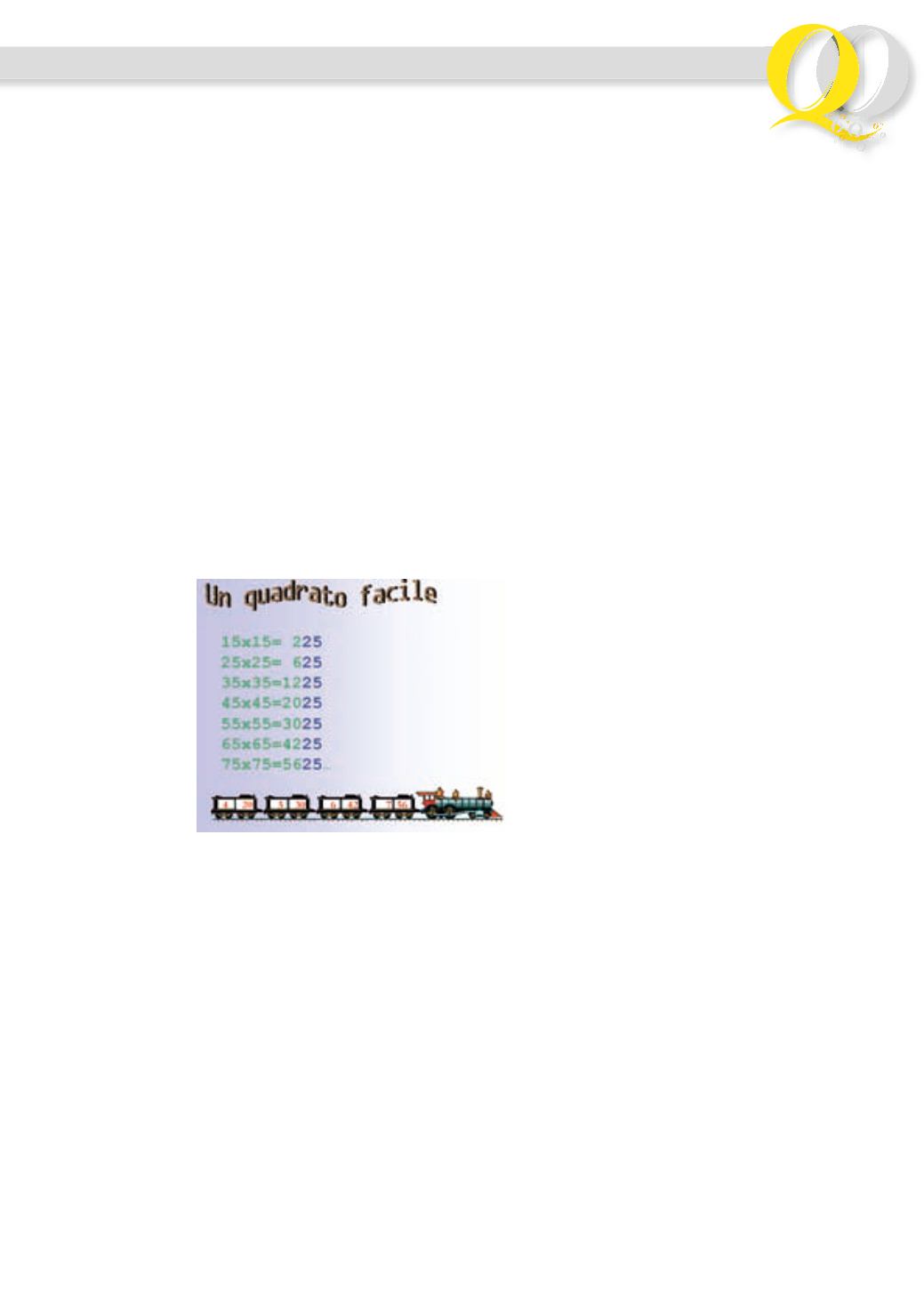
La prima cosa che dovrebbe balzare
all’occhio sono le ultime due cifre:
sempre 2 e 5. Adesso cerchiamo di
scoprire come si comportano le prime
cifre. Ci sono tante risposte diverse.
Qualcuno nota che la colonna delle
centinaia è composta solo da 2, 6 e 0,
che seguono sempre la sequenza 2 6
2 0 0. E questa osservazione è esatta.
Ma se uno volesse calcolare il quadra-
to, ad esempio, di 905, dovrebbe fare
troppi calcoli. Altri studenti notano
che la differenza fra i vari valori au-
menta via via di 2 unità, cioè fra 2 e 6,
l’aumento è di 4; fra 6 e 12, l’aumento
è 6; fra 12 e 20, l’aumento è 8, e poi
10, 12, 14…
Anche questa osservazione, co-
munque esatta, non aiuta a trovare
il quadrato di un numero alto. Allora
osserviamo che le prime due cifre
del quadrato son date dalla cifra del
primo numero di partenza, moltipli-
cata per il suo successivo. E questa
conclusione ci permette di scrivere
direttamente il quadrato di un nu-
mero che termina per 5.
Se qualche ragazzo avesse avuto
difficoltà a scoprire il meccanismo,
gli propongo il problema con una
presentazione che lo può mettere
più a suo agio: i trenini. È una mia
invenzione con la quale faccio scopri-
re il meccanismo e lo studente delle
elementari deve dire la regola con la
quale sono scritti i numeri nei finestri-
ni di ciascun vagone. Quando lo sco-
laro è tranquillo per averne già risolti
alcuni, gli propongo il seguente, di
cui capirà facilmente il meccanismo
col quale 4 diventa 20 e 7 diventa 56
(vedi figura 2).
Ripetiamo la regola appena scoper-
ta: per fare il quadrato di un numero
che termina per 5, basta coprire il 5,
e quello che rimane va moltiplicato
per il suo successivo, e poi al risultato
si attacca 25 in fondo.
Esempi:
Il quadrato di 85 vale 8x9
(cioè 72), con 25 in fondo, cioè 7225.
Il quadrato di 195 vale 19x20 (si può
fare a mente, vale 380), con 25 in fon-
do, cioè 38.025. Il quadrato di 705 vale
70x71 (farà 4970, poiché 70x70=4900),
con 25 in fondo, cioè 497.025.
Tra i vari numeri che possiamo ana-
lizzare, proviamo con quelli che sono
formati da alcuni 9 e un 5 finale. Il
quadrato di 95 vale 9x10 (cioè 90),
con 25 in fondo, e quindi 9.025. Il qua-
drato di 995 vale 99x100 (è banale
trovarlo amente, 9900), con 25 in fon-
do, e quindi 990.025. Analogamente,
il quadrato di 9995 vale 99.900.025.
Scriviamo a questo la regola che
possiamo arguire osservando gli ul-
timi tre quadrati trovati: il quadrato
di un numero composto da alcuni
9 e da un 5 finale, è composto dal
medesimo numero di 9 del numero
di partenza, poi un numero uguale
di 0, e in fondo 25.
Allora il quadrato del nostro
999.995 (composto da cinque cifre
9), sarà formato da cinque cifre 9, al-
Figura 2


